该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Description

本题给出平面上 $n$ 个点的坐标，第 $i$ 个点的坐标是 $(x_i, y_i)$。定义两点的斜率为：$\frac{y_i - y_j}{x_i - x_j}$，也就是纵坐标之差除以横坐标之差。本题保证这 $n$ 个点的横坐标各不相同。

你的任务是：从这 $n$ 个点中选出恰好 $k$ 个点，使得最大化这 $k$ 个点两两之间的斜率的最小值。也就是说，你需要求出如下的式子的值：

$$\max \limits_{|S| = k} \{ \min \limits_{i, j \in S, i \neq j}\frac{y_i - y_j}{x_i - x_j} \}$$

其中 $S$ 表示你所选择的点的集合， $|S|$ 表示你选择的集合内的元素个数。

Format

Input

本题有多组测试数据。

第一行一个正整数 $T$，表示数据组数。

对于每一组数据，第一行两个正整数 $n$、$k$，分别表示总点数和你需要选择的点数。接下来 $n$ 行，每行输入两个数 $x_i,y_i$ ，表示这个点的坐标。

Output

对于每一组数据，输出一行一个实数，表示答案。

• 请保留六位小数

你的答案与标准答案之间的相对误差或绝对误差不超过 $10^{-6}$ 时视为答案正确。

Samples

2
4 3
1 2
2 4
3 3
4 1
2 2
1 1
5 3

-1.000000
0.500000

样例解释

第一组样例，如下图所示，红色的为选择的点：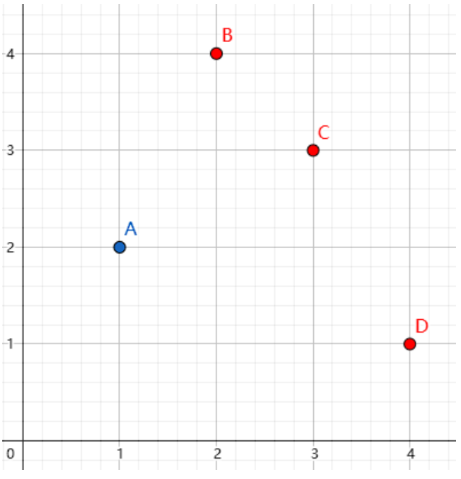

最小的斜率出现在点 C 与点 D，斜率为 $-2.0$ 。如果把 D 点换成 A 点，那么最小的斜率出现在点 B 与点 C，斜率为 $-1.0$。所以最优方案是选择 A,B,C。

第二组样例，每个点都要选择进去。

Limitation

• 对于 30% 的数据，$2\leq k \leq n \leq 10$，保证单个测试点 $\sum n \leq 10$。
• 对于 60% 的数据，$2\leq k \leq n \leq 1000$，保证单个测试点 $\sum n \leq 1000$。
• 对于 100% 的数据 ，$1\leq T \leq 100,2\leq k \leq n \leq 10^5, 0\leq x_i, y_i \leq 10^9$，保证单个测试点 $\sum n \leq 10^5$。

保证所有点的横坐标各不相同。